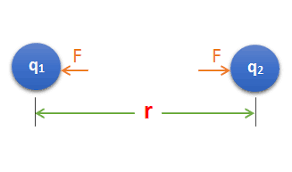
Este simulador muestra en esquema y gráficamente la relación que hay entre la fuerza de atracción entre dos cargas eléctricas, una positiva y una negativa, y la distancia que las separa. Mediante controles se puede modificar la magnitud de las cargas y la distancia que las separa. Las cargas se pueden cambiar de posición ya sea acercándose o alejándose.En el lado derecho se muestra la gráfica de la función F(r) mostrando con un punto rojo el valor particular de la simulación.
El estudio de la fuerza entre cargas eléctricas fue formulada en 1780 por Charles-Augustin de Coulomb.
La ley de Coulomb, expresa la magnitud de la fuerza de atracción o repulsión entre dos cargas eléctricas en función de la cantidad de carga y la distancia entre ellas. Su expresión matemática es:
$$F=k\frac{q_1q_2}{r^2}$$
La fuerza entre dos cargas puntuales (sin dimensión) es directamente proporcional al producto de las magnitudes de las cargas e inversamente proporcional al cuadrado de distancia entre ellas.
$$F\alpha q_1$$
$$F\alpha q_2$$
$$F\alpha \frac{1}{r^2}$$
Para establecer la igualdad, se requiere una constante de proporcionalidad cuyo valor dependerá de las unidades en que se mida las magnitudes: fuerza, carga eléctrica y distancia. En el Sistema Internacional, la unidad de fuerza es el Newton (N), la de distancia es el metro (m) y la de carga eléctrica es el Coulomb (C), para estas unidades, la constante de proporcionalidad conocida como constante de Coulomb o constante electrostática tiene un valor de: $k=\frac{1}{4\pi\epsilon}Nm^2/C^2=9\times 10^9Nm^2/C^2$ para el vacío. Si las cargas se encuentran en el aire, el valor de la constante es prácticamente la misma, pero en otros materiales hay que tener en cuenta su constante dieléctrica.
Como puede observarse, la magnitud de la fuerza depende de 3 variables, el applet permite establecer los valores de las cargas y analizar la función de la fuerza respecto a la separación de las cargas. Esta función es una función racional
$$F(r)=C\frac{1}{r^2}$$
donde $C=9\times 10^9 q_1q_2$
El dominio de la función en este contexto queda limitada a valores positivos de r $D_F=(0,\infty)$