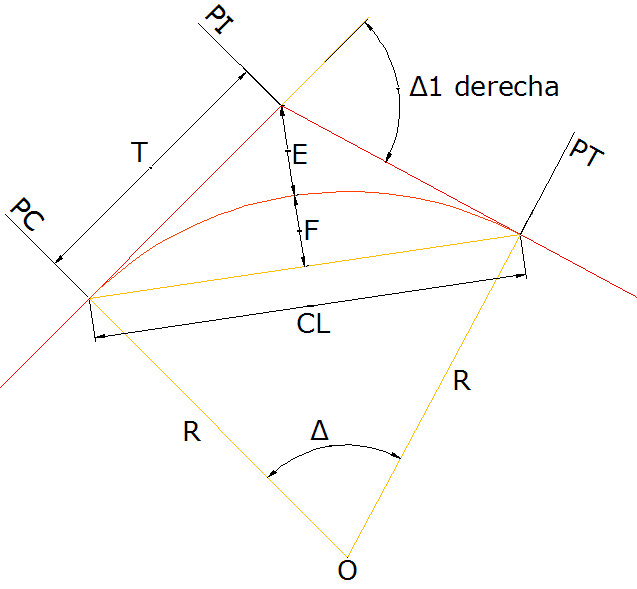
Este ejercicio consta un applet que simula el alineamiento horizontal de una curva circular simple, Mediante trazos geométricos se muestra que el ángulo central tiene la misma medida que el ángulo de deflexión de la cuerda. Mediante controles se puede modificar la dirección de las rectas tangentes de entrada y salida a la curva y el radio de la curva.
Conceptos sobre una curva circular simple
- Alineamiento Horizontal
El alineamiento horizontal de una carretera es la proyección de la línea central de ésta sobre un plano horizontal.
- Curva circular simple
Una curva circular simple está formada por dos rectas tangentes unidas mediante una circunferencia.
- Grado de Curvatura $C_c$
Es el ángulo central que abarca un arco de 20 m.
$$\frac{G_c}{360°}=\frac{20}{2\pi r}$$- Longitud de la curva circular $L_c$
Es la longitud del arco circular que enlaza las dos rectas tangentes. Se calcula a partir del grado de curvatura y el ángulo central.$\Delta_c$
$$\frac{L_c}{20}=\frac{\Delta _c}{G_c}$$
- Longitud de un arco sobre la curva circular $l$
Es la distancia entre el punto de inicio de la curva, PC, y un punto cualquiera, P, sobre la curva.
- Deflexión de un punto P sobre la curva $\theta$
Es el ángulo que forma la prolongación de la tangente en el punto de inicio de la curva PC y la tangente en el punto P.
$$\frac{\theta}{G_c}=\frac{l}{20}$$
- Ángulo de la cuerda $\phi$
Ángulo comprendido entre la prolongación de la tangente y la cuerda considerada.
$$\phi=\frac{\theta}{2}$$
- Cuerda $c$
Recta comprendida entre dos puntos de la curva como por ejemplo PC y P.
$$c=2r sin\phi$$
- Cadenamiento
Es el procedimiento para trazar una carretera a base de segmentos rectos poligonales de 20 m de longitud. Se denomina así porque antiguamente se utilizaba una cadena de dicha longitud para realizar la medición
Para trazar una curva simple de una carretera, se utiliza la trigonometría. Los ángulos de deflexión de un punto y de la cuerda pueden medirse tanto desde el centro como desde la circunferencia. Cuando la curva tiene un radio muy grande, muchas veces el acceso al centro es complicado o imposible.
Una curva suave se presenta cuando la transición de un tipo de curva a otro no forma picos, esto ocurre cuando la derivada de las funciones que forman ambas curvas tienen la misma pendiente en el punto de intersección.
La función que describe la parte positiva de la circunferencia es circunferencia con centro en el origen es $f(x)=\sqrt{r^2-x^2}$ y la función que describe la recta tangente a la circunferencia en un punto$(x_0,y_0)$ es $f(x)=m(x-x_0)+y_0$
La condición de curva suave se presenta cuando $f'(x)=g'(x)$
$$-\frac{x}{\sqrt{r^2-x^2}}=m$$